ここ最近ディープラーニングの発展が著しい。chatGPTに代表される生成系AIは、ぱっと見人間が書いた文章に遜色ないほどの完成度になっています。
画像・動画生成においてもdeepfakeやAIグラビアなるものが登場しており、実在の人物さながらのクォリティを誇っています。
ただなぜディープラーニングがこれほどまでに上手くいくかを理論的に説明することはできていません。現在ディープラーニングのパラメータは千億(\(\sim 10^{11}\))と言われており、ある入力に対して、個々のパーセプトロンを追っていても全体としてどのような出力になるか分かりません。
こうした大量の個々のもつミクロな状態たちに統計的な処理をしてマクロな状態を予想する、という手法は物理学ではすでに発見されています。すなわち統計力学です。統計力学の考え方を触れることで、ディープラーニングがうまくいく理由の参考になるかもしれません。まずは統計力学にふれていきます。
このあたりの詳細は以下の書籍が参考になります。以下の本を読み、インスピレーションを受けて本記事を記載してます。内容自体は以下の書籍とは直接の関係はないことご了承ください。
1. 統計力学の概要
統計力学について、概要を説明していきます。
1-1 多粒子系の状態
古典物理学(=解析力学)によると、ある粒子1つの状態というのは位置座標\(\ \boldsymbol{q}=(q_x,q_y,q_z)\)と運動量\(\ \boldsymbol{p}=(p_x,p_y,p_z)\)を指定することで一意に決めることができます。原則任意の物理量は\(\ (\boldsymbol{q},\boldsymbol{p})\)を用いて表すことができるからです。例えば、エネルギー\(\ E\)、角運動量\(\ L\)は
\[
E=\frac{\boldsymbol{p}^2}{2m}+V(\boldsymbol{q}),\ \ \ L =\boldsymbol{q}\times \boldsymbol{p}
\]
というように\(\ (\boldsymbol{q},\boldsymbol{p})\)を用いて表すことができます。ここで\(\ V(\boldsymbol{q})\)はポテンシャルエネルギーで例えば、弾性エネルギーであれば\(\ V(\boldsymbol{q}) \sim q^2\)、重力であれば\(\ V(q) \sim q^{-1})\)
いずれにせよ1粒子の場合状態を確定するための変数の合計数は、位置\( (q_x,q_y,q_z)\)と運動量\( (p_x,p_y,p_z)\)で6つとなります。1粒子の状態はこの6つの変数で作られる6次元空間の点として表され、状態変化は6次元空間の軌跡として表現されます。
この6次元空間を物理学では位相空間といいます。数学の位相空間論における位相空間とは全くの別物で、それと区別して相空間ともいわれます。ここでは相空間とします。
では次に2つだった場合を考えます。このとき2つの粒子の位置/運動量をそれぞれ、\(\ (\boldsymbol{q}^1, \boldsymbol{p}^1)\)、\(\ (\boldsymbol{q}^2,\boldsymbol{p}^2)\)とします。簡単のため質量は同じにします。すると例えば2粒子のエネルギー、角運動量の合計は
\[
E=\frac{\boldsymbol{p}_1^2}{2m}+\frac{\boldsymbol{p}_2^2}{2m}+V(\boldsymbol{q}_1,\boldsymbol{q}_2)
=\sum_{i=1}^2 \frac{\boldsymbol{p}_i^2}{2m}+V(\boldsymbol{q}_1,\boldsymbol{q}_2)\\
L = \boldsymbol{q}_1\times \boldsymbol{p}_1+\boldsymbol{q}_2\times \boldsymbol{p}_2
=\sum_{i=1}^2 \left(\boldsymbol{q}_i\times \boldsymbol{p}_i\right)
\]
2粒子における状態を確定するための変数の合計数は\(12\)個になります。相空間は12次元となり、2粒子の状態変化は12次元の相空間の軌跡となります。
最後にいっぱいある時を考えます(\( N \sim 10^{23}\))。といっても2粒子と同様で、例えば全エネルギー/全角運動量は
\[
E=\sum_{i=1}^N \frac{\boldsymbol{p}_i^2}{2m}+V(\boldsymbol{q}_1,\boldsymbol{q}_2,…,\boldsymbol{q}_N)\\
L=\sum_{i=1}^N \left( \boldsymbol{q}_i\times \boldsymbol{p}_i \right)
\]
\(N\)粒子系の状態を表すための変数の数は\(3N\)個になります。\(N\)粒子系の状態変化は\(3N\)次元という超巨大な相空間の軌跡で表されます。
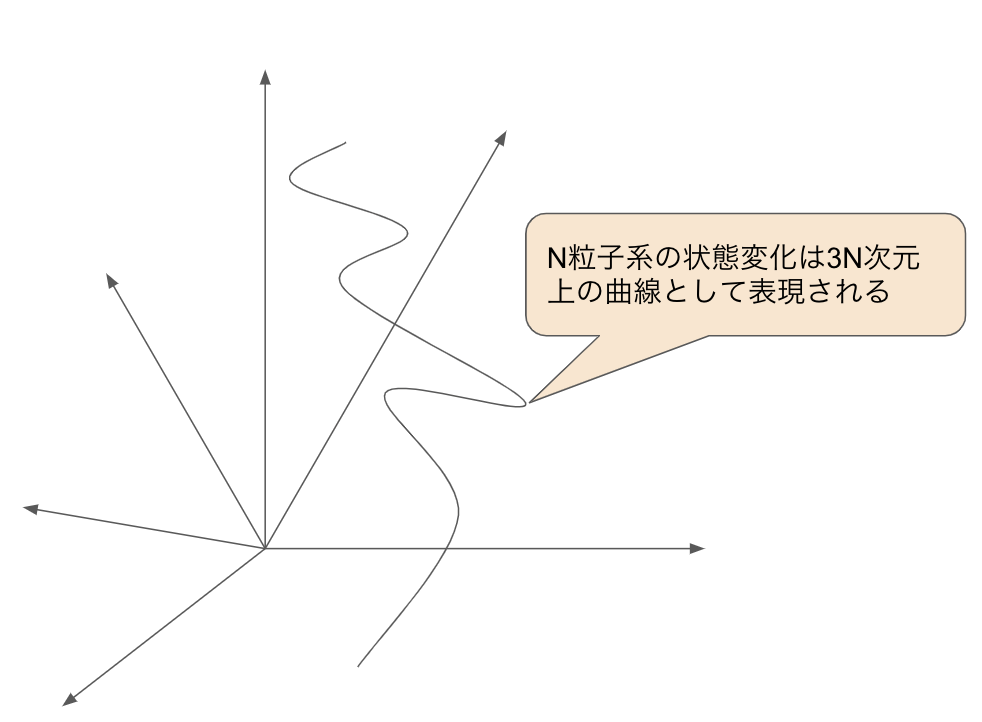
※厳密にいうとエネルギー保存則などの各種保存則のため、数次元小さい空間になりますが、\(3N\)からみると無視でき、かつ本論の本質とは関係ないで、ここでは考慮しないものとします。
1-2 統計力学
\(N\)粒子系の状態変化は\(\ 3N\)次元相空間における軌跡であることは前節の通りですが、ここで1つの仮定なし要請を行います。これはエルゴード仮説と呼ばれているもので、「\(\ 3N\)次元相空間の各点に対応する状態の確率はすべて等しい」というものです。まぁ普通に考えて至極当然といえば当然ですが、これは実は証明されているわけではないので仮説となってます。
※このあたり気になる方は「等重率の仮説」や「エルゴード理論」とかで調べてみてください。以下の田崎さんの統計力学が参考になります。
\( 3N\)次元相空間の点\(\ \xi\in \mathbb{R}^{3N}\)の周りの微小体積は\( W(\xi)d\xi\)とすると、全体の体積\(V\)は\[
V = \int_{\mathbb{R}^{3N}}W(\xi)d\xi
\]と計算できます。
このときある物理量\(X\)というものは、\(\ 3N\)次元相空間上のある関数\(\ X:\mathbb{R}^{3N}\ni \xi \rightarrow X(\xi)\in \mathbb{R} \)に対応し、その平均、分散\[
E(X) = \frac{1}{V}\int X(\xi) W(\xi)d\xi\\
V(X) = \frac{1}{V} \int \left( X(\xi)-E(X) \right)^2 W(\xi)d\xi
\]をもつ量になります。
この考え方を統計力学ではミクロカノニカル分布といいます。
2. ニューラルネットワーク
さて次に、深層学習のベースとなっているニューラルネットワークについて、数理的な観点で見ていきたいと思います。
2-1 多層パーセプトロン
まずニューラルネットワークの要素となる個々のパーセプトロンです。これらの解説はネットに溢れているので、ここではざっくりにします。
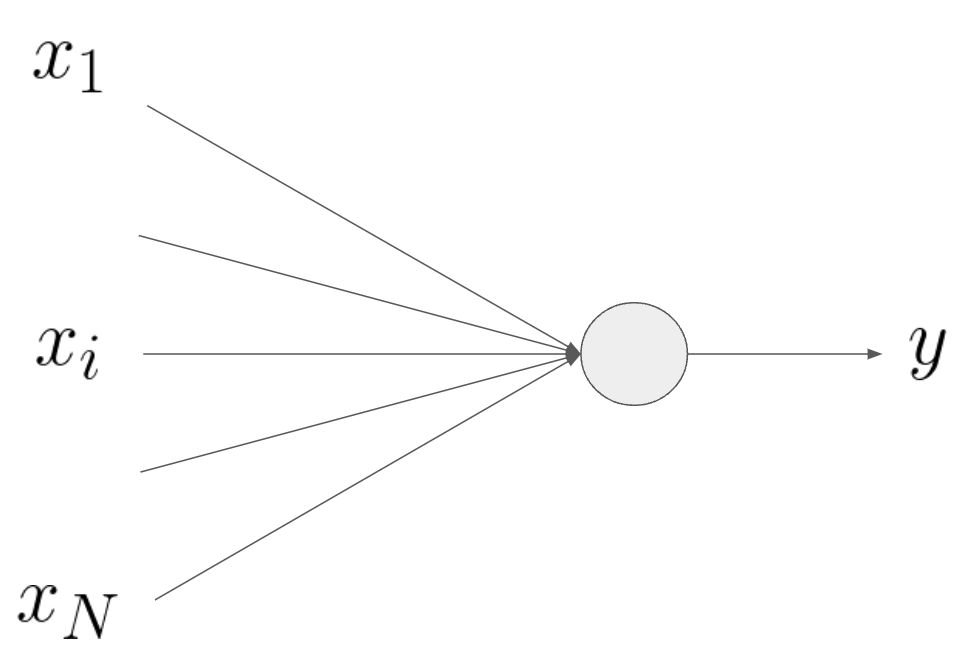
\(N\)個の入力データをまとめて\(\mathbf{x} = (x_1,…,x_N)\)のベクトルで表記します。重み係数を\(\mathbf{w}=(w_1,…,w_N)\)、バイアスを\(b\)とし、活性化関数を\(\ f:\mathbf{R}\ni u\rightarrow f(u)\in\mathbf{R}\)とすると、パーセプトロンの出力\(y\)は\[
y = f(\mathbf{w}\cdot\mathbf{x}+b)
\]となります。
次にパーセプトロンが1つの層になっている場合を考えます。といっても単独のパーセプトロンとほとんど同様です。
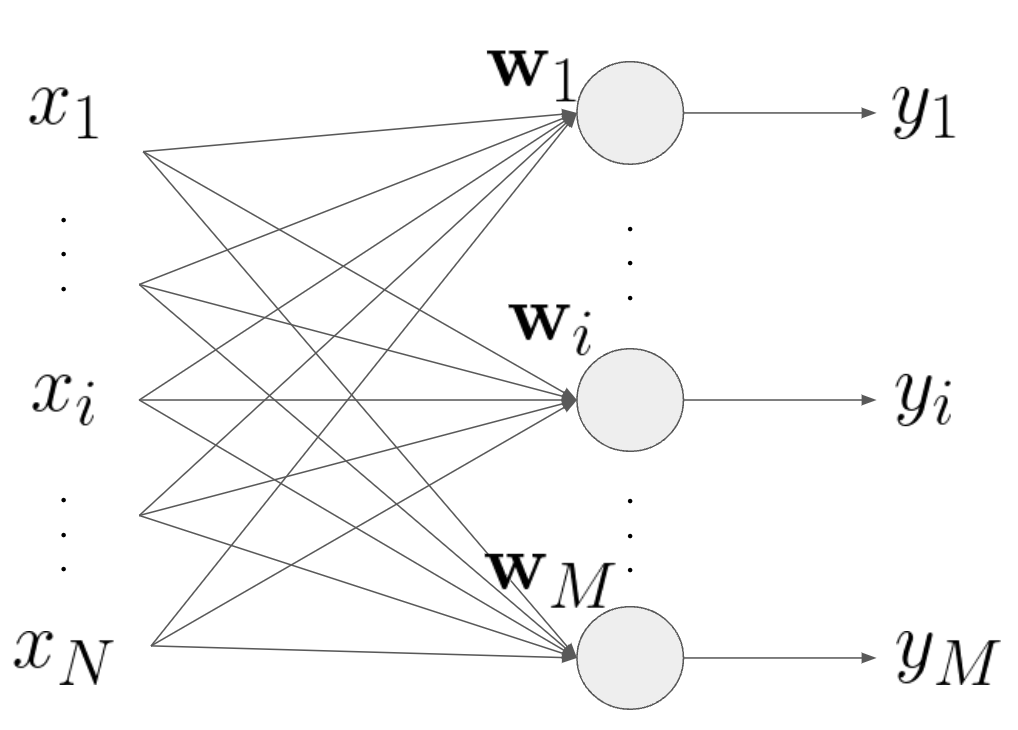
\( i\in\{1,..,M\}\)とすると、出力の集合は\[
y_i = f(u_i),\ \ i\in\{1,..,M\}\\
\ u_i \equiv \mathbf{w}_i\cdot\mathbf{x}+b_i =\sum_{j=1}^{N}w_{ij}x_j+b_i
\]となります。
次に多層パーセプトロンの場合です。添字が多くて分かりづらいですが、やっていることは同様です。
層\(\ell\in\{0,..,L\}\)の入力\(\mathbf{x}^{\ell-1}\)、重み係数を\( w^{\ell}=(\mathbf{w}_1^{\ell},..,\mathbf{w}_i^{\ell},…,\mathbf{w}_{N_{\ell}}^{\ell} ) \)、出力を\(\mathbf{x}^{\ell}\)とします。\(\ell = 0\)は入力データを表すことにします:\( \mathbf{x}^0=\mathbf{x}\)。
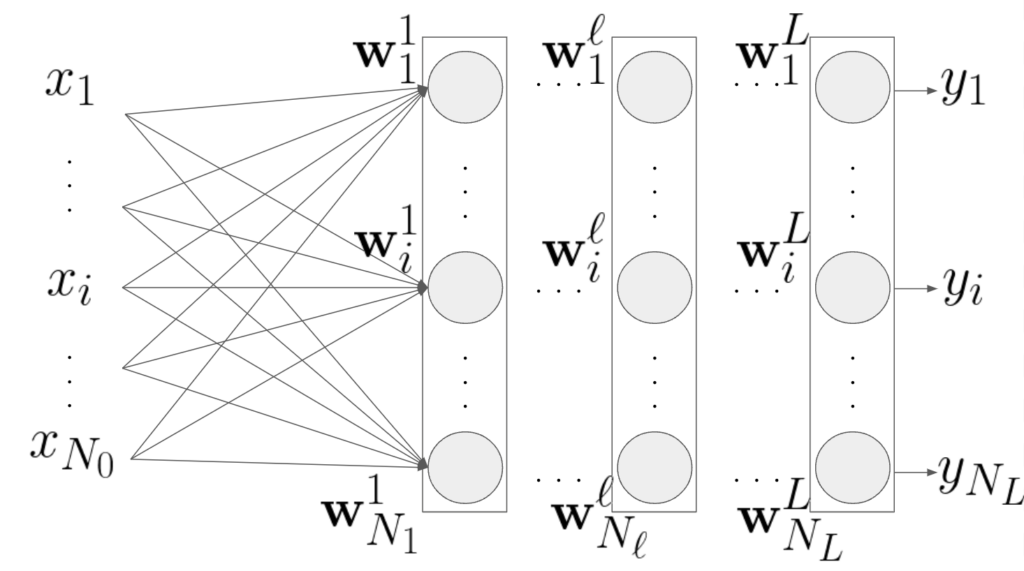
このとき最終層の出力\(y_i\)は\(L\)階の合成関数になります。学習とは教師データと出力データを比べ、微分のチェーンルールを用いて各重み係数ベクトル\(\mathbf{w}_i^{\ell}\)やバイアス\(b_i^{\ell}\)を調整する作業になります。
2-2 ニューラルネットの相空間
さて、ここのパーセプトロンの状態は、重み係数ベクトル\(\mathbf{w}_i^{\ell}\)やバイアス\(b_i^{\ell}\)で決まることができます。chatGPTなどの大規模言語モデル(LLM)ではこれらのパラメータが数百億~数千億、\( ( \sim10^{12})\)ほど存在することになります。これら個々のパーセプトロンの状態を追いかけても、ディープラーニングがうまくいく理由は見えてこないと思われます。
そこで統計力学にならってディープラーニングの相空間を考えます。パラメータをひとつにまとめて
\[
\theta = \{\mathbf{w}_i^\ell,b_i^{\ell}\}, \ \ i\in \{1,..,N_{\ell},\ \ \ell \in\{1,..,L\}\}
\]
とおきます。\(N\)粒子系の相空間と同様に考えて、ニューラルネットの状態変化は\(\{\theta\}\)のなす相空間内で軌跡を描くととらえます。
さらにこの空間に構造を入れることができ、多様体になり、特殊な幾何構造を導入し、解析可能となります。いわゆる情報幾何の考えですが、そろそろ長くなってきたので、一旦ここまでにします。
3. まとめ
本稿でニューラルネットがうまくいく理由を統計力学になぞったらうまくいくかもということを謳ってみました。もちろんそう簡単には上手くいかないとは思いますが、アイディアとしては悪くないかなと思い、記事にしてみました。
本稿はかなり個人の意見が強いので、あくまで参考程度にしてもらえればと思います。
最後まで読んでいただきありがとうございます。
質問等はコメント欄かお問合せにてよろしくおねがいいたします。