こんにちは、今回は交流電源にコンデンサーを繋いだときの電圧と電流の位相差を求めていきましょう。
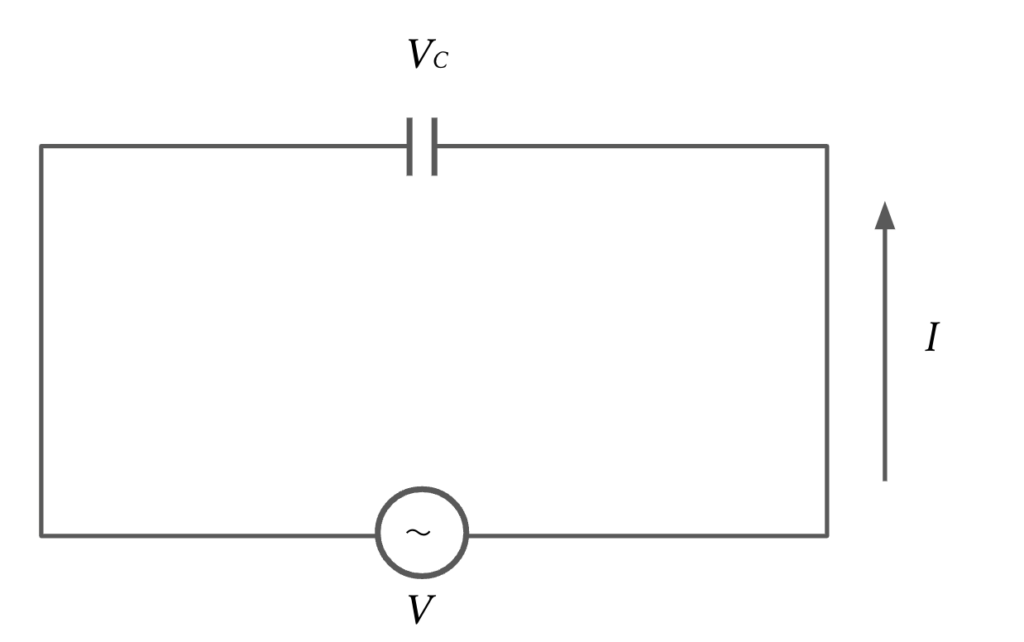
数学Ⅲを使った高校物理4と同様、反時計回りを正とし、交流電源を
\[V(t) = V_0\sin\omega t\]
とします。Qをコンデンサーの電気量、Cを電気容量とすると、電位差は\(Q/C\)と表せます。したがってキルヒホッフ則より、
\[
V(t)-\frac{Q}{C} = 0 \tag{1}
\]
となります。ここで電流は電気量の時間変化の極限で表現できましたから、
\[
I= \frac{dQ}{dt}
\]
となります。(1)の両辺を時間tで微分すると
\[
\frac{dQ}{dt} = \frac{d}{dt}CV(t) = CV_0\omega\cos\omega t
\]
つまり
\[I(t) = CV_0\omega\cos\omega t\]
であることがわかります。これをsinで表すと
\[I(t) = CV_0\omega\sin\left(\omega t + \frac{\pi}{2}\right)\]
となります。数学Ⅰで出てきたように、\(y=f(x)\)を右へ𝑎だけ平行移動すると\(y=f(x-a)\)となることを使えば、位相に着目すれば電圧を\(\pi/2\)左へ平行移動すると電流の位相に一致することがわかります。電流は交流電圧にくらべ\(\pi /2\)進むことがわかります。
今回は短めですが、以上です。
最後まで読んでくださりありがとうございます。
質問等はコメント欄もしくはお問合せにておねがいいたします。