今日はこちらで少し触れた、テンソル場についてすこし解説していきます。
- ざっくり定義
まずテンソルについてです。テンソルをざっくり一言でいうなれば、「多次元配列のようなもの」です。この記述は、特定条件下では正しく、最近流行の機械学習ライブラリのTensorFlowを使う分には困らないので、まずは多次元配列的になものと考えてもらって差し支えないです。
多次元配列のイメージは以下になります。
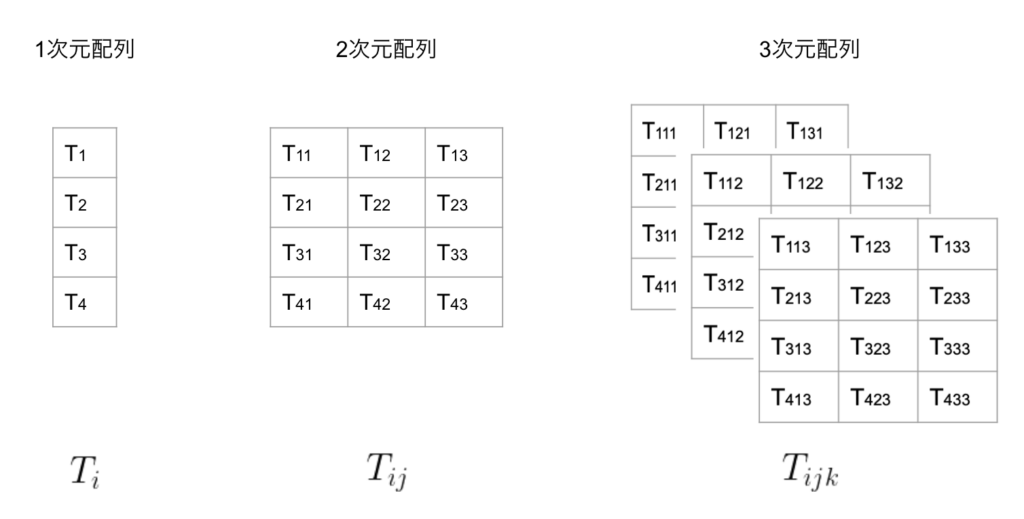
4次元以上はうまく図示できないですが、その各要素の表現は3次元配列\(T_{ijk}\)から添字がひとつ増えて、\(T_{ijkl}\)になります。
で、テンソル場は、時空の各点にテンソルが存在する場のことです。配列の各要素は、時空の各点に依存して値が変わるものです。テンソルを2次元の配列(すなわち行列)としたときのイメージ的には以下のようになります。
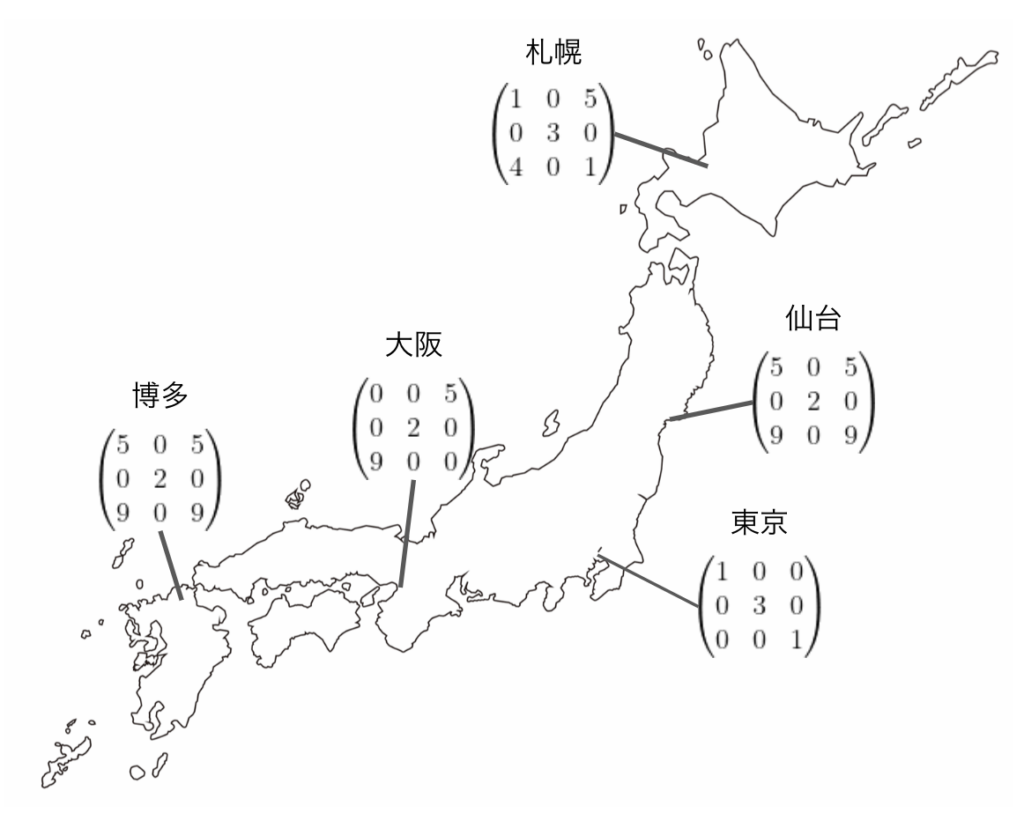
日本の各地で異なるテンソル値をもち、さらに時間経過に対しても変わるような場をテンソル場といいます。
したがってテンソル場は各時空に依存する多次元配列なので、配列の要素を指定する文字\(i,j,k,…\)と時空に依存する量なので\(T_{ijk..}(t,x,y,z)\)と表現できます。上記の例ですと2次元配列なので、\(T_{ij}(t,x,y,z)\)となります。
- 数学的に厳密な定義
これを少し数学的に見ていきます。
まずテンソルの定義からお話します。線型空間(ベクトル空間ともいいます)を\(V\)とし、\(V\)上の線型写像\(f:V\rightarrow \mathbb{R}\)を汎関数といいます。汎関数全体\(\{f\}\)の集合を\(V^*\)とします。\(V^*\)を\(V\)の双対空間といいます。
テンソルは
\[T:\underbrace{V^* \times V^*…..\times V^*}_{p} \times \underbrace{V\times V….\times V}_{q}\rightarrow \mathbb{R} \tag{1}\]
なるような多重線型写像として定義されます。厳密には\((p,q)\)型テンソルといいます。
上にあげた図の例ですと\((0,2)\)型テンソルですので\(T_{i,j}\)と書ける、というようなイメージです。
テンソル場の定義はというと、、、ちょっと多様体が出てきたりして悩ましいんですが、、
ざっくりは局所的には\(\mathbb{R}^n\)にみなせる空間を多様体といいます。多様体は滑らかに曲がっているので、線型空間をいくつも貼り合わせてできるイメージです。はり合わせるのに使う線型空間を接空間と呼びます。拙い図ですみませんが、イメージ的には下記のようになります。
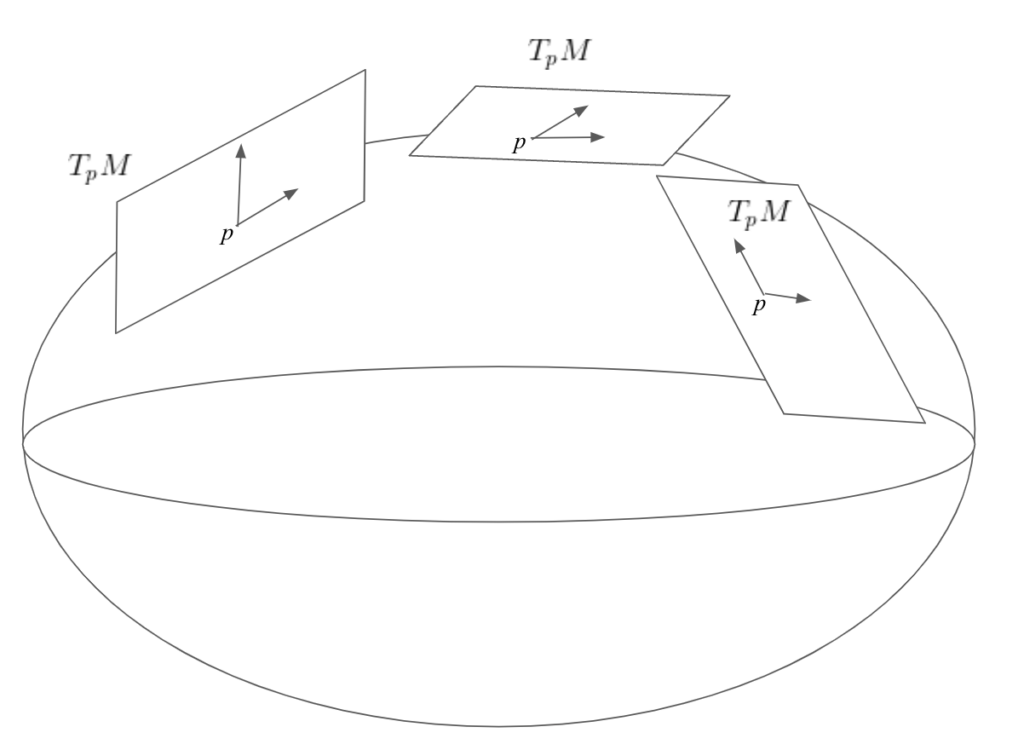
線型空間をはり合わせてつくる、つまり多様体の各点に線型空間が存在するイメージです。
\(M\)を多様体とし、多様体の点\(p\in M\)上の接空間を\(T_p M\)とします。
接空間\(T_p M\)の双対空間を\(T_p^*M\)とします。\(T_p M\)は線型空間となりますので、(1)の定義で\(V=T_pM\)と選ぶことができます。したがって点\(p\in M\)における\((a,b)\)型のテンソル場は
\[
T:\underbrace{T_p^*M \times T_p^*M…..\times T_p^*M}_{a} \times \underbrace{T_pM\times T_pM….\times T_pM}_{b}\rightarrow \mathbb{R}
\]
となります。
具体的に\((0,2)\)型テンソル場を考えてみます。
\(T_pM\)は線型空間でしたから、基底を指定できます。これを\(\{e_i\}_i\)とおきます。ゆえ\(T_pM\)の任意の元は\(\sum_i A^i e_i\equiv A^i e_i\)とかけます。
(もちろん\(A^i,e_i\)は多様体の点\(p\)にも依存するのですが、添字が煩雑になるので、略してます。)
すると定義域は\(T_pM\times T_pM \ni A^ie_i \times A^je_j=A^iA^je_i\times e_j\)となります。これに写像\(T\)をかますと\(\mathbb{R}\)になるわけですから、写像\(T\)は基底\(e_i\times e_j\)を打ち消す要素をもつことになります。これは写像\(T\)が\(e_i\times e_j\)の双対基底で展開できることを意味し、\(e_i\)の双対基底を\(\omega^i\)とすれば
\[
T=T_{ij} \omega^i \times \omega ^j
\]
とかけます。この\(T_{ij}\)がテンソルの成分表示であり、多次元配列で表せることになります。
つまり「テンソル場は定義の通り基底に依存しない幾何学的実体」であり、「テンソル(場)は基底を決めて初めて成分表示できる」ことになります。物理学ではテンソルを成分のみで表示することが多いですが、これは基底を暗黙のうちに決めている、もしくは時空の各点で不変としているためと考えられます。
- テンソルの例
テンソル場の身近な例はなかなかないので、、きびしぃところですが、、いくつかあげてみます。
1)計量テンソル
いきなりぶっこんでますが、基本的なテンソル場なのであげておきます。ややこしいですが、計量テンソルという名前ですが、テンソル場になります。多様体Mの点\(p\in M\)上の計量テンソル\(g_p\)は\((0,2)\)型テンソル場となります。すなわち
\[
g_p = g_{\mu\nu}\omega^\mu\times \omega^\nu
\]
とかけます。特殊相対論や場の量子論では\(g_{\mu\nu}\)は時空の各点で一定とみなすので、\(g_{\mu\nu} = \mathrm{diag}(1,-1,-1,-1)\)となります。一般相対論では多様体の各点に依存するので\(p\)の関数になります。
2)電磁テンソル
これまた身近な例ではないので、悩ましいのですが、、
電磁気学によると電場と磁場は相互補完的な位置付けになり、光は電場と磁場が振動しあいながら進む電磁波になることが示されます。
これは電場と磁場とひとまとめに扱えるかもというアイディアにつながり、それを実現したものが電磁テンソルになります。電磁テンソルは計量テンソルと同様\((0,2)\)型テンソルのテンソル場になります。したがって\[F=F_{\mu\nu}\omega^\mu \times \omega ^\nu\]のような形になり、その成分\(F_{\mu\nu}\)を行列で表すと
\[F_{\mu\nu} =\begin{pmatrix}
0& E^x/c& E^y/c &E^z/c \\
-E^x/c& 0& -B^z& B^y \\
-E^y/c& B^z & 0& -B^x \\
-E^z/c& -B^y & B^x& 0
\end{pmatrix}
\]
というような感じになります。ここで\((E^x,E^y,E^z)\)は電場で\((B^x,B^y,B^z)\)は磁場で、cは光速となります。
3)リーマン曲率テンソル
ゴリゴリの微分幾何になってくるので、割愛します。。
4)応力テンソル
こちらも連続体力学を説明しないといけないので割愛します。。
なかなかテンソルのいい例が思いつかず、、
本日はこれくらいにしておきます。
最後まで読んでくださりありがとうございます。
質問等はコメント欄かお問い合わせにておねがいいたします。