量子コンピュータを勝手に解説する記事 トポロジカル量子計算について3

こんにちは、前回に続きトポロジカル量子計算をゆるく解説していきます。

本稿はエニオンのフュージョンから、各種量子ビットを構成していきます。
※今回もこちらを参考にしてます。

1)おさらい

さて、絶対零度で各エニオンが無限に離れているという理想的な環境では以下のことが成立しました。

・非可換エニオン系の基底状態は縮退しており、動的な散逸がない。
・局所的な操作ではエニオンの状態を制御できない。これは局所的な摂動の影響を受けないことを表している。
・エニオンを組み替え(braiding)することで、系の状態をコヒーレントに時間発展させることができる。これはエラーは非局所的な摂動によってのみ発生することを意味する。エニオンをロバストな組み替え(braiding)をすることで量子ゲートは実装されるが、量子ゲートは$F$-行列や$R$-行列といったトポロジカルな性質のみに依存しているため、理想的な環境では実質的にエラーは発生しないこととなる。

一方通常の量子ビットでは、

・系の基底状態はほとんどの場合縮退していない。
・系のハミルトニアンが局所的な摂動にセンシティブ。
・演算も局所的な量子ゲートによってなされるが、ハミルトニアンが局所的な摂動にセンシティブであるため、エラーが発生しやすい。絶対零度という理想的な状況でも、「零点振動」してるがゆえ局所的な摂動を抑えることは原理的に不可能。

となるので、トポロジカル量子計算は従来の量子計算に比べ、ハードウェアレベルでエラーが抑制されることになります。

2)量子ビットの構成

前回から引き続きイジングエニオンを用いて量子ビットを構成していきます。

※もちろんフィボナッチエニオン系でも量子ビットを構成することは可能です。が、ヒルベルト空間全体をエニオンの部分空間の単純なテンソル積で表すことができない等イジングエニオン系より複雑です。基本的な考え方はどちらも同様なため、今回はイジングエニオンを用いていきます。

はじめに真空の状態からエニオンを生成するとします。このときフュージョン則$\sigma \times \sigma = 1 + \psi$となることから、２つのエニオンが真空から生成される過程は
$$|\sigma\sigma;1 \rangle$$
となり、４つのエニオンが生成される過程は
$$|\sigma\sigma;1 \rangle|\sigma\sigma;1 \rangle \ \mathrm{ or } \ |\sigma\sigma;\psi \rangle|\sigma\sigma;\psi \rangle$$ の２通りになります。これを図示すれば以下のようになります：

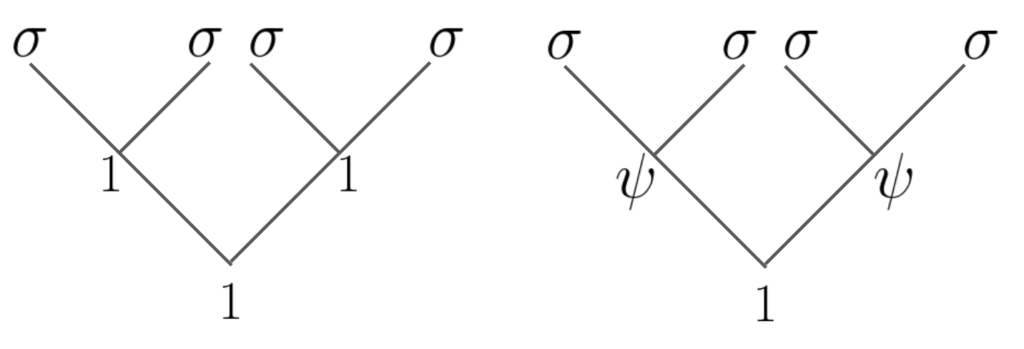
この２つの過程は直交しているので、これらに計算基底を割り当てることが可能となります。すなわち

$$\begin{align} &|0\rangle = |\sigma\sigma;1 \rangle|\sigma\sigma;1 \rangle\\ &|1\rangle = |\sigma\sigma;\psi \rangle|\sigma\sigma;\psi \rangle \end{align}$$

という形です。同様にさらに６つのエニオンの場合は

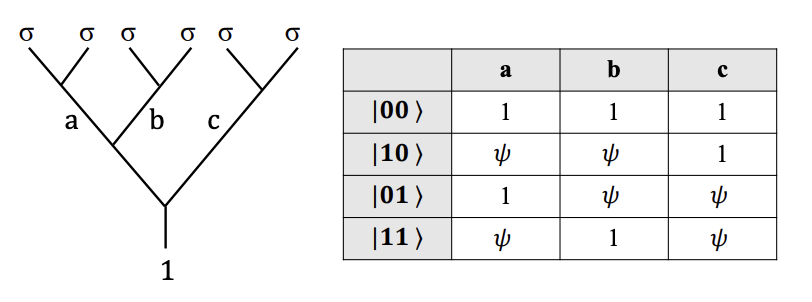
※この図はこちらのFIgure.7から抜粋

という4通りの過程が存在し、それぞれの過程に計算基底を以下のように割り当てます：

$$\begin{align} &|00\rangle = |\sigma\sigma;1 \rangle|\sigma\sigma;1 \rangle|\sigma\sigma;1 \rangle \\ &|10\rangle = |\sigma\sigma;\psi \rangle|\sigma\sigma;\psi \rangle|\sigma\sigma;1 \rangle \\ &|01\rangle = |\sigma\sigma;1 \rangle|\sigma\sigma;\psi \rangle|\sigma\sigma;\psi \rangle \\ &|11\rangle = |\sigma\sigma;\psi \rangle|\sigma\sigma;1\rangle|\sigma\sigma;\psi \rangle \end{align}$$

一般にエニオンが$2N$個あれば、生成過程は$2^{N-1}$通り存在し、$N-1$個の量子ビットを構成できることになります。

以上から真空からエニオン系を生成するにはいくつかの過程があることがわかりますが、エニオンの生成過程が量子ビットを構成することになります。エニオン系はいくつかの生成過程が重ね合わさることで、一般の量子ビットが構成されることになります。

3)量子ゲート

量子ビットは構成できたので、次に量子ゲートについて考えていきます。

トポロジカル量子計算における量子ビットの操作は、エニオンのフュージョン過程を操作することに相当します。実はこれはすでにこちらで登場しており、$F$-演算子や$R$-演算子です。これらをうまく組み合わせて量子ゲートを構成します。

例えば、1量子ビットの$X$-ゲートや、$Z$-ゲートは、$F^{-1}R^2F, R^2$の行列表現を見れば明らかなように

$$X=F^{-1}R^2F, \ \ Z=R^2$$

と与えられます。

2量子ビットの場合も同様にして、以下で与えられます。
※$R_{ij}$はエニオン$i$とエニオン$j$を交換する交換演算子とします。

$$\begin{align} &X_1=R_{23}^2 = F^{-1}R^2F \otimes \mathbb{I}\\ &X_2=R_{45}^2 = \mathbb{I}\otimes F^{-1}R^2F \\ &Z_1=R_{12}^2 = R^2\otimes \mathbb{I} \\ &Z_1=R_{56}^2 = \mathbb{I} \otimes R^2 \end{align}$$

同様にアダマールゲートや制御NOTゲートも以下で与えられます。

$$\begin{align} &U_{H,1}=R_{12}R_{23}R_{12}=RF^{-1}RFR\otimes \mathbb{I}\\ &U_{H,2}=R_{56}R_{45}R_{56}=\mathbb{I}\otimes RF^{-1}RFR \\ &U_{CZ}=R_{12}^{-1}R_{34}R_{56}^{-1} \end{align}$$

これらを図示したのが以下になります。

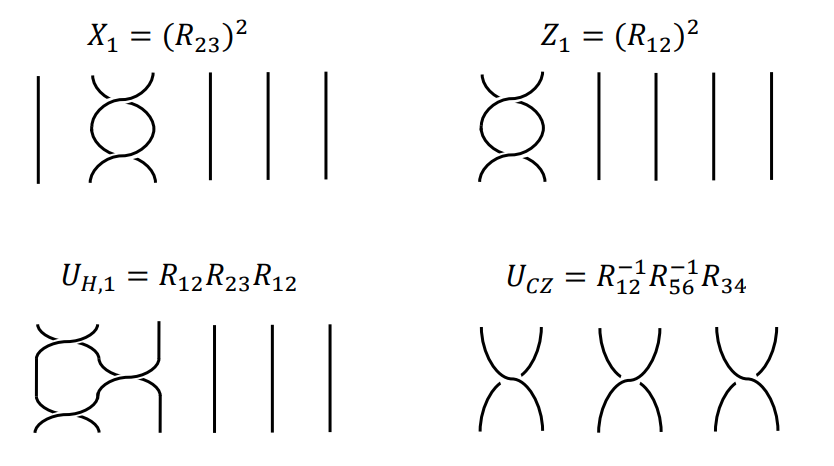
※図はこちらのFigure8より抜粋

以上より主要な量子ゲートを構成することができました。

ただし、これまであげた$X,Z,U_H,U_{CZ}$といったゲートはクリフォード群をなす量子ゲートにあたります。しかし、ゴッテスマン・ニルの定理によると、クリフォード群からユニバーサルなゲートを構成することはできないため、任意の量子回路を実現するにはさらに非クリフォードゲートを加える必要があります。トポロジカル量子計算においては、非クリフォードゲートは２つのエニオンを近づけることで実装されます。これは本稿の最初に記載した通り、基底状態の縮退が解かれることを意味し、縮退が解かれた際のエネルギー準位差を$\Delta E$とすると、非クリフォードゲートは
$$U= \begin{pmatrix} 1 & 0 \\ 0 & e^{i\Delta E t}\\ \end{pmatrix}$$ で与えられます。$\Delta E t$をうまく制御することで、任意の位相差を与えるゲートが作られる、という形になります。

4)測定

最後に量子ビットの測定について説明します。トポロジカル量子計算での量子ビットの測定は、エニオンのフュージョン過程を測定することに相当します。イジングエニオン系では、$\sigma\times\sigma = 1+\psi$より、真空かフェルミオン1つが生成するかの２択になりますが、これらはエネルギー準位が異なるため、観測可能となる、というイメージです。

例えば、2)量子ビットの構成の2量子ビットの場合で説明すると、第一ビットを$Z$-基底で測定して、
・エネルギー準位に変化なし：エニオン1,2に射影演算子$|0\rangle \langle 0| \otimes \mathbb{I}$を作用させたことに相当
・エネルギー準位に変化あり：エニオン1,2に射影演算子$|1\rangle \langle 1| \otimes \mathbb{I}$を作用させたことに相当

という感じになります。

5)まとめ

少し長くなってきたので、今回はここまでにしたいと思います。

前回までの知識を用いてイジングエニオンを用いて具体的に量子ビットと量子ゲートを構成してみました。

最後まで読んでいただきありがとうございます。
質問等はコメント欄かお問合せにてよろしくおねがいいたします。