こんにちは、本日は条件付期待値について勝手に解説します。
本稿はこちらで紹介した保江さんの確率論を参考にしてます。
1)準備
まず期待値などを定義します。
DEF.4 確率変数の期待値
確率空間\( (\Omega,\mathcal{F},P) \)上の確率変数を\(X\)とする。このときルベーグ積分\[
E[X]=\int_{\Omega}X(\omega)P(d\omega)
\]を\(X\)の期待値という。さらに\[
V[X]=E\left[ (X-E[X])^2\right]
\]を\(X\)の分散という。
ちなみに分散は\[
V[X]= E [ (X-E[X])^2 ]
\\=E \left[ X^2 -2 XE[X] + E[X]^2 \right]
\\=E[X^2]-2E[X]E[E[X]]+E[E[X]^2]
\\=E[X^2]-E[X]^2
\]と変形することが可能です。
次に独立を定義します。
DEF.5 独立
確率空間\( (\Omega,\mathcal{F},P) \)上の確率変数を\(X,Y\)とする。\(X,Y\)が独立であるとは、任意の事象\( A,B \in \mathcal{F} \)に対して、\[
P\{\omega \mid X(\omega) \in A \cap Y(\omega)\in B \}
=P\{ \omega \mid X(\omega)\in A\}\times P\{ \omega \mid Y(\omega)\in B\}
\]が成り立つときをいう。
いくつか期待値の性質をまとめておきます。これらは定義をもとに計算していけばすぐ導出できますので、証明は省略します。
THM.1 期待値の性質
確率空間\( (\Omega,\mathcal{F},P) \)上の確率変数を\(X,Y\)とする。以下が成り立つ。\[
E[aX+bY]=aE[X]+bE[Y]\\
V[aX]=a^2V[X]
\]
確率変数\(X,Y\)が独立である場合、さらに以下が成り立つ。\[
E[XY]=E[X]E[Y] \\
V[X+Y]=V[X]+V[Y]
\]
2)条件付き期待値
さて条件付き期待値について定義していきます。通常だと絶対連続やラドン・二コディムの定理を用いて定義するのですが、ここでは少し変わった定義を行います。
2-1)平均と分散の再定義
分散が存在する条件は\[
E[X^2]=\int_{\Omega}|X(\omega)|^2 P(d\omega) < \infty
\]となりますが、これは\(X\)が自乗可積分であることを意味します。つまり\(X\in L^2(\Omega , \mathcal{F},P) \equiv L^2(\Omega) \)となり、分散をもつ\(X\)の全体はヒルベルト空間をなすことになります。
もちろん分散が存在しないような確率変数というのも存在しますが、かなり特殊なケースですので、上記条件を課しても問題はない感じです。
確率変数\(I\)を\[
I:\Omega\ni \omega \rightarrow I(\omega)=1\in \mathbb{R}
\]とする写像とすると、\(E[I]=\int P(d\omega ) = 1\)となり\(I \in L^2(\Omega)\)となります。これを用いると、平均は\[
E[X]=E[X\cdot I]=\int_{\Omega}X(\omega )\cdot I(\omega) P(d\omega)=\langle X, I \rangle
\]より、確率変数\(I\)との内積と表すことができます。
また分散は\[
V[X]=E[X^2]-E[X]^2=\int_{\Omega}X(\omega)^2 P(d\omega)-E[X]^2
=\|X\|^2- \langle X, I \rangle^2
\]と表され、\(X\)のノルムと\(I\)との内積で表されることになります。
2-2)ヒルベルト空間の適用
確率変数\( \{X_i\}_i \)が互いに独立で、平均\(0\)で分散が\(1\)である場合、\[
E[X]=0, E[X_i X_j]=\langle X_i,X_j\rangle = 0
\\ V[X]= \langle X_i,X_i\rangle=1
\]となることから、クロネッカーのデルタを用いて\[
\langle X_i , X_j\rangle = \delta_{ij}
\]とすることができます。これは\( \{X_i\}_i \)が完全正規直交系をなすことを意味します。すなわち任意の確率変数\( A\in L^2(\Omega) \)に対して、ある\(\{a_n\}_n\)が存在して、\[
A=\sum_{n}a_n X_n
\]と書くことができます。
ヒルベルト空間の性質として、直和分解がありました。これは任意の\(X\in L^2(\Omega)\)に対して、ある\(X_1,X_2\in L^2(\Omega) \)、\(\langle X_1,X_2\rangle = 0\)が存在して、\[
X=X_1+X_2
\]と分解できることを意味します。\(M\subset L^2(\Omega)\)を、射影作用素\(P_M: L^2(\Omega)\rightarrow P_M(L^2(\Omega)) =M\subset L^2(\Omega)\)による、\(L^2(\Omega)\)からの射影とすると\[
L^2(\Omega) = M \oplus M^{\perp},
\\ M^{\perp}=\{ X \in L^2(\Omega) \mid \langle X,X’ \rangle=0,X’\in M \}
\]と直和分解できる、ということになります。
\( X_1,X_2,… \)を確率変数列とし、その生成族\( \sigma [\{X_i\}_i] \)を1次結合全体で定義します。すなわち\[
\sigma [\{X_i \}_i] = \left\{ \sum_{i}a_i X_i \mid a_i\in \mathbb{C},X_i\in L^2(\Omega) \right\}
\]とします。
2-3)条件付き期待値の定義
さて、上記までの事柄を使って条件付き期待値を定義します。
DEF.6 条件付き期待値
\(X_1,X_2,…\)を確率変数列とし、その生成族を\( M=\sigma [\{X_i\}_i]\)とする。
もし\( X\in L^2(\Omega)\)が\[
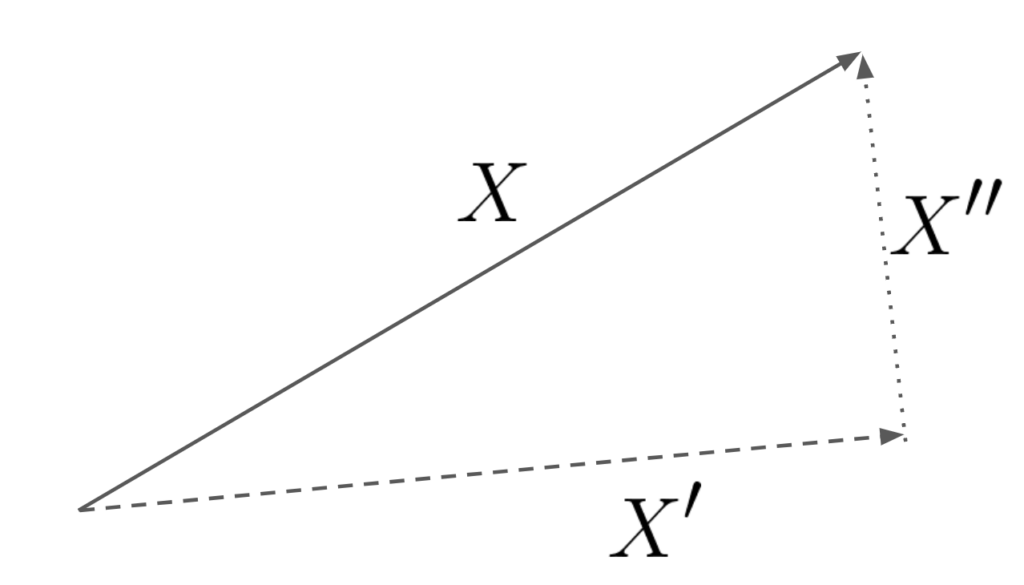
X=X’+X”,\ X’\in M, \ X”\in M^{\perp}
\]と直和分解できるとき、\(X’\)を生成族\(M\)に関する\(X\)の条件付き期待値といい、\[
X’=E[X\mid M]
\]と表す。
さらに\(X\)が指標関数\(\chi_A\)であるとき、\[
P_M(A)=E[\chi_A\mid M]
\]と表し、条件付き確率という。
\(X’,X”\)は直交するため、\(M\)の中で\(X\)の最も良い近似が\(X’=E[X\mid M]\)であることを主張しています。図で表すと以下のイメージになります。
本日はここまでにします。
最後まで読んでいただきありがとうございます。
質問等はコメント欄かお問い合わせにてよろしくおねがいいたします。