ε-δ論法について

こんにちは、$\varepsilon$-$\delta$について解説していきます。

まずは数列の極限からです。数列の場合は$\varepsilon$-$N$法とも呼ばれています。

数列の収束は
$$\lim_{n\rightarrow\infty}a_n = a$$
と書かれましたが、これを$\varepsilon$-$N$で表すと
$$\forall \varepsilon >0,\exists N\in \mathbb{N}:\forall n >N \Rightarrow |a_n -a |< \varepsilon$$
となります。同じことですが日本語で書くと、

「任意の$\varepsilon > 0$に対して、ある$N$が($\varepsilon$に依存して)存在して、もし$n >N$ならば、$|a_n-a| < \varepsilon$が成り立つ。」

になります。もうすこし補足すると、「$0$より大きい、どんな数$\varepsilon$を持ってきても、それに対応する$N$があって、その$N$より大きい$n$だったら、収束値$a$と$a_n$とのずれは$\varepsilon$より小さくなる」という感じです。

これは初見だとクラクラしてくるかと思いますが、以下これの意味を解説します。

例えば
$$a_n = \frac{n}{n+1},\ n\in\mathbb{N}$$
となる数列を考えてみましょう。この数列は$1/2,2/3,3/4,4/5….$となる数列で$n\rightarrow \infty$で$1$に収束となる数列となります。

毎度拙い図ですみませんが、図であわらすと以下のようなイメージになります。

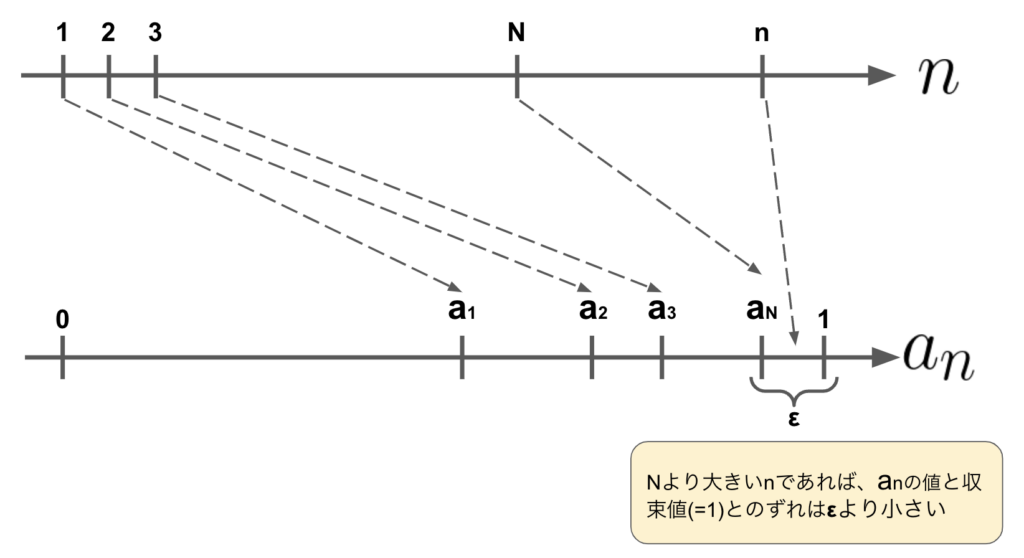
まず$\varepsilon$の値を決めます。これは収束値との誤差の値を意味で、要はこれくらいならずれててもいいという値です。英語で誤差をerrorと呼びますが、これは数学者コーシーによって、先頭のeをギリシア文字化して$\varepsilon$にしたのが始まりのようです。

今$\varepsilon = 10^{-4}$としてみます。とすると
$$|a_n-a| < \varepsilon \Leftrightarrow \left| \frac{n}{n+1}-1 \right| < 10^{-4}$$
となり、整理すると$n>10^{4}-1$となります。つまり$N=10^{4}-1$となり、$\varepsilon = 10^{-4}$に対して、$N = 10^{4}-1$がきまったことになります。

$\varepsilon = 10^{-4}$では、全然誤差の範囲じゃない、ということであれば、$\varepsilon = 10^{-10}$としてみましょう。とすると同様に計算して$N=10^{10}-1$が得られ、$n>N=10^{10}-1$ならば$|a_n-1| < 10^{-10}$が成り立つことがわかります。

それでも足りないということであれば、$\varepsilon =10^{-10000000000}$にしてみます。これも上記と同様に$n > N=10^{10000000000}-1$なら、$|a_n-1| < \varepsilon$が成り立ちます。

以上から、「$0$より大きければ、どんな実数$\varepsilon$をもってきても、必ずその$\varepsilon$に対応する $N$が存在し、$n>N$に対して、$|a_n -1| < \varepsilon$になる」ことがわかります。

今回は数列$a_n = n/(n+1)$を例にしましたが、一般に具体的な$N$は数列によって変わります。これを見つけるのが$\varepsilon$-$N$法の証明方法のキモになります。

さて、実際に解析する場合ですと、収束先がわからない場合も多々あります。そんなときは収束するかどうかから吟味が必要になります。その吟味する際に使うのがコーシー列というものです。

数列$a_n$がコーシー列であるとは、$\forall \varepsilon >0$に対して、$\exists N$が存在して、$n,m > N$だったら、$|a_n-a_m|< \varepsilon$が成り立つときをいいます。

まぁ端的に言って、収束値が$a$だったのを、十分大きい$m$での$a_m$にしただけになります。収束するのであれば、十分大きい$n,m$であれば、その差$|a_n-a_m$も十分小さくなるよというものです。

先ほどの
$$a_n=\frac{n}{n+1}$$
がコーシー列かどうかみてみます。

とりあえず$\varepsilon = 10^{-10}$程度に考えておきます。このとき$m>n>N$とすると
$$\left|a_n-a_m\right|=\left|\frac{n}{n+1}-\frac{m}{m+1}\right| <\left|\frac{n}{n+1}-1\right|=\left| \frac{-1}{n+1}\right|<\frac{1}{n}$$
となります。$1/n$は明らかに収束するので、$\varepsilon$に対して$N$が存在して、$n>N$ならば$1/n<\varepsilon$が成立します。したがって、
$$\left|a_n-a_m\right| < \epsilon$$
が成り立ちます。ゆえに$a_n$はコーシー列になります。

コーシー列を使うメリットは収束先が不明な場合も使える点です。実際に解析を行うとき収束先は未知の場合が多いです。そのときまず収束するか、発散するかを吟味する必要がありますが、そんなときに使われます。
収束先が不明なケースというのはかなり出てきます。実数や複素数に値をもつ数列であれば、あまり気にならないですが、関数を全て集めてできた集合上の数列、すなわち関数列を相手にすると、収束先が未知であることが多々あります。

収束先が不明な場合、万が一対象の空間からはみ出てしまう場合もあります。これは都合が悪く、はみ出ないようないい感じの性質を抽象化できないか、ということで考えられたものがこちらで定義した完備、という概念になります。

なお、はみ出るというのはどういうことかというと、例えば以下のような漸化式を見てみます。

$$a_1 = \frac{3}{2},\ a_{n+1} = \frac{a_n^2+2}{2a_n}$$
$\{a_n\}_n$は全ての$n\in\mathbb{N}$で有理数になりますが、この収束値は$\sqrt{2}$の無理数になり、有理数からはみ出てしまう、といった感じです。

ちなみに収束値が$\sqrt{2}$になる理由は、高校数学の範囲で十分示せます。
収束値を$a$とすれば、特性方程式から$a = (a^2+2)/2a \Leftrightarrow a^2 =2$で、$a_n > 0$であるから、$a=\sqrt{2}$。ゆえに、 $$a_{n+1}-\sqrt{2} = \frac{(a_n-\sqrt{2})^2}{2a_n}<\frac{a_n}{2a_n} (a_n-\sqrt{2})= \frac{1}{2} (a_n-\sqrt{2}) < \frac{1}{2^n}(a_1-\sqrt{2})\rightarrow 0 \ (n\rightarrow \infty)$$

上記の方法で極限を扱う手法は、一般に$\varepsilon$-$\delta$と呼ばれていますが、これは数列に限らず、連続性や微分など極限を扱うもの全般で使われます。このあたりはまた別の記事に書こうかと思います。

最後まで読んでいただきありがとうございます。
質問等はコメント欄かお問い合わせにておねがいいたします。