サラリーマンが測度論を勝手に解説する無謀な記事２

前回、測度空間まで導入しました。今回は可測空間上の写像、可測関数を考えます。

測度空間を\((\Omega,\mathcal{F},\mu)\)とします。といってもとりあえず、
・\(\Omega\):区間\([0,1]\)
・\(\mathcal{F}\):区間\([0,1]\)の内部に含まれる区間をすべて集めてきた集合。\( \left\{[0.2,0.3],[1/3,1/2],[1/\sqrt{3},1/\sqrt{2}],……\right\}\)的なイメージ
・\(\mu\):区間の幅を出力する関数
と思ってもらっていいです。

さて、\(\Omega\)上の実数値関数\(f:\Omega\ni \omega \rightarrow f(\omega)\in X\)について、考えてみます。\(f\)の定義域\(\Omega\)は可測空間という、測度をふれる特別な集合でした。せっかく苦労してもたせた性質なので、\(f\)によって写された後も同じように測度をふれる構造をもった集合であってほしいと考えるのは自然なことかと思います。
実はこれが可測関数の考え方で、測度をふる条件が整った空間、すなわち可測空間から可測空間への写像を可測関数ないし可測写像といいます。

具体的に区間と幅で考えてみやす。

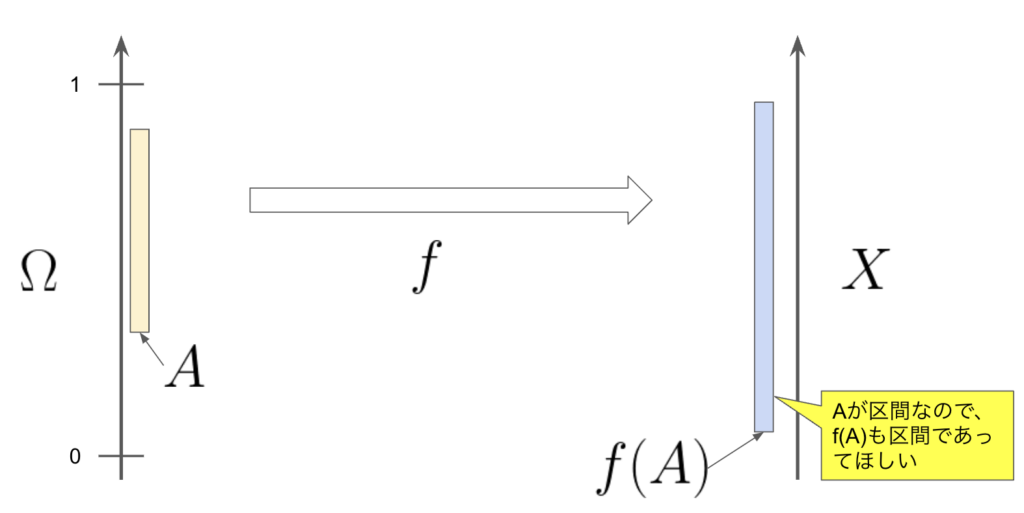
\(A\)を\(\Omega\)の内部のある区間とします(\(A\in \mathcal{F}\))。\(A\)自体は集合なので、\(f(A)\)は像、すなわち集合になります。この\(f(A)\)がすべて\(X\)の区間となっていればよい、という感じです。

ただ、上の場合だと\(X\)の区間で、\(f(A)\)に対応しない区間が存在できてしまい、都合が悪いです。そのため\(X\)側に注目するように変更します。\(X\)の内部の区間を\(B\)とすると、全ての\(B\)に対して、\(f^{-1}(B)\)が\(\Omega\)の区間になっていればよい、ということにします。以下のイメージです。

これを数学的に書くと以下になります。

DEF.3 可測写像
\((\Omega,\mathcal{F}),(X,\mathcal{G})\)を可測空間とする。写像\(f:\Omega\rightarrow X\)が任意の\(B\in\mathcal{G}\)に対して、 \[\left\{\omega \in \Omega | f(\omega)\in B \right\}\equiv f^{-1}(B)\in\mathcal{F}\] をみたすとき、\(f\)を可測写像、もしくは可測関数とよぶ。

これが可測関数の考え方になります。

可測関数の定義を見れば明らかですが、可測関数は測度がふられてなくても定義できる概念です。

すこしそれますが、位相空間における連続写像\(f:X\rightarrow Y\)も可測空間における可測関数と同じように、写した前後で構造or性質を変えたくないという考えで定義しています。それが可測性か連続性かの違いだけになります。定義を書くと

連続写像
\( (X,\mathcal{O}(X)),(Y,\mathcal{O}(Y)\)を位相空間とする。写像\(f:X\rightarrow Y\)が任意の開集合\(V\in \mathcal{O}(Y)\)に対して、
\(\{x\in X | f(x) \in V \}\equiv f^{-1}(V) \in \mathcal{O}(X)\)となるとき、\(f\)を連続写像という。

といった感じで、かなり定義が似ていることがわかります。

ちなみに位相空間の開集合が可測集合となるようなσ加法族を考えることができます。このσ加法族は無数にあるのですが、そのうち最小のものをボレル集合族といいます。

本日はここまでにします。次回は測度と可測関数を用いて、積分を定義していきます。

最後まで読んでいただきありがとうございます。
質問等はコメント欄かお問い合わせにておねがいします。